Qcm 9 cc 2016

Bonjour,
Je ne comprend pourquoi pour l’énoncé suivant, dans la réponse on utilise 2T/r et non pas 2T/2r car comme c’est une hémisphère on devrait diviser par 2 non ?
De plus peut-on parler de loi de laplace quand on utilise la constante T ?

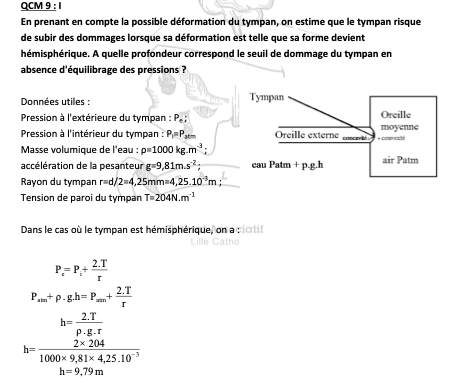
Sujet : Prenons maintenant en compte la possible déformation du tympan. On estime que le tympan risque de subir des dommages lorsque sa déformation est telle que sa forme devient hémisphérique. A quelle profondeur correspond le seuil de dommage du tympan en absence d'équilibrage des pressions ?

Hello !
J'ai peur d'avoir mal compris ta question, mais je tente une réponse
J'imagine que r Est le rayon du tympan. Si sa déformation Est hemispherique, elle s'inscrit donc dans une sphère de rayon r (Si tu accolais deux tympans déformés l'un à côté de l'autre, tu aurais une sphère complète de rayon r). Or c'est la définition même de la loi de Laplace, qui prend en compte la différence de pression entre concavite et convexite, indirectement dû au rayon de courbure. Ici le rayon de courbure est bien égale au rayon du tympan
Si T est la constante élastique du tympan (ou un truc approchant), oui tu peux utiliser La place. Tu auras une surface de démarcation entre deux fluides, marquée par un angle de courbure.
Si Ça peut t'aider, c'est un cas similaire à celui du tube en U : interface eau / air (souvent prise hemispherique également).
Est ce que c'est,mieux ?
Bon courage

Bonjour,

D'après la correction on doit trouver 9,79. Je trouve 11,5m. J'ai beau le faire et le refaire avec des parenthèses et sans, je trouve tjr 11,5.



Merci d'avance !

Salut ! Hésites pas à simplifier !

2x204 / 1000x9,81x4,25x10^-3 = 408/(9,81x4,25) car 1000x10^-3 = 1
Et ça te donne bien 9,79
Par contre fait gaffe aux priorités opératoires, par exemple si tu tapes sur ta calculatrice 408/9,81x4,25 alors tu obtiens le résultat de (408/9,81)x4,25 et ce sera faux

C'est good ?

PS : oublie pas de dormir