ED 3 Ex 1 ex 2 et ex3
2 participants
Page 1 sur 1
 ED 3 Ex 1 ex 2 et ex3
ED 3 Ex 1 ex 2 et ex3
Hello,
Alors je suis paumée sur ce 3ème ED il y a plusieurs questions sur lesquelles je bloque.
Dans l'exercice 1 question 1 je ne comprends pas pourquoi on fait la racine de s dans le calcul de e/s.
Dans la question suivante, la question 2, je ne comprends pas pourquoi on fait la racine de 448/racine de36 ? et d'où est ceque sort mon 0,50 ??? Car à la fin on fait 0,50 - alpha/2
Dans l'exercice 2, question f) je ne trouve pas 1,02 pour le test de student quelqu'un pourrait me détailler le calcule? je comprends pas pourquoi ils disent un ddl = 25 t= 1,02 alors que quand on regarde sur la table pour ddl=25 c'est 2,06 ?
Dernière question, pour l'exercice 3, est-ce qu'on pourrait me détailler le calcul pour la question car je n'arrive pas non plus à aboutir à ce résultat.
car je n'arrive pas non plus à aboutir à ce résultat.
Merci beaucoup.
Alors je suis paumée sur ce 3ème ED il y a plusieurs questions sur lesquelles je bloque.
Dans l'exercice 1 question 1 je ne comprends pas pourquoi on fait la racine de s dans le calcul de e/s.
Dans la question suivante, la question 2, je ne comprends pas pourquoi on fait la racine de 448/racine de36 ? et d'où est ceque sort mon 0,50 ??? Car à la fin on fait 0,50 - alpha/2
Dans l'exercice 2, question f) je ne trouve pas 1,02 pour le test de student quelqu'un pourrait me détailler le calcule? je comprends pas pourquoi ils disent un ddl = 25 t= 1,02 alors que quand on regarde sur la table pour ddl=25 c'est 2,06 ?
Dernière question, pour l'exercice 3, est-ce qu'on pourrait me détailler le calcul pour la question
Merci beaucoup.
Marwa- Messages : 12
Date d'inscription : 30/11/2020
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
Yo!
Il s'agit du 3ème ED de licence ou de paces ?
Il s'agit du 3ème ED de licence ou de paces ?
Vault- Messages : 132
Date d'inscription : 20/09/2018
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
Merci!
Je n'ai pas la correction donc j'espère que les indications suivantes t'aideront malgré tout.
1) L'énoncé nous donne la valeur de la variance (s²). Or, on a besoin de la valeur de l'écart-type (s) pour notre calcul.
Cependant, la variance n'est rien d'autre que le carré de l'écart-type. De cette manière s = racine(s²).
Je n'ai pas la correction donc j'espère que les indications suivantes t'aideront malgré tout.
1) L'énoncé nous donne la valeur de la variance (s²). Or, on a besoin de la valeur de l'écart-type (s) pour notre calcul.
Cependant, la variance n'est rien d'autre que le carré de l'écart-type. De cette manière s = racine(s²).
Vault- Messages : 132
Date d'inscription : 20/09/2018
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
2) Dans cette question, on cherche à trouver un pourcentage de chance d'observer une moyenne dans un certain intervalle.
Etant donné que l'on travaille avec une moyenne, il est nécessaire d'utiliser les valeurs qui lui sont associées.
Ici, on n'utilise pas simplement la valeur de l'écart-type s mais la valeur de l'écart-type de la moyenne s/racine(N).
Ci-joint une réponse donnée auparavant qui explique la distinction entre ces deux écart-types pour mieux comprendre :
https://talc.forumgratuit.org/t10547-ecart-type-de-la-moyenne?highlight=moyenne
Pour résoudre cet exercice, on utilise la table de l'écart-réduit, qui nous permet de trouver le pourcentage que l'on recherche.
La particularité de la table de l'écart-réduit, c'est qu'elle ne nous permet pas de trouver la probabilité de se situer dans un pourcentage mais la probabilité de s'en trouver en dehors.
De plus, selon une répartition normale, la répartition des valeurs de l'échantillon étudié est symétrique de part et d'autre de la moyenne.
Cela signifie que l'on trouve 50% des valeurs à gauche de la moyenne et 50% des valeurs à droite de la moyenne.
Cependant, l'intervalle que l'on recherche n'est pas établit symétriquement par rapport à la moyenne (61).
On devra donc procéder par 2 étapes pour aboutir au résultat.
Un schéma peut nous aider à visualiser la situation :

On recherche donc la probabilité de se situer en dessous de l'intervalle (alpha1 / 2) et la probabilité de se situer au-dessus de l'intervalle (alpha2 / 2).
On recherche les valeurs de alpha grâce aux valeurs d'Epsilon :
Probabilité de se trouver en dessous :
Epsilon1 = e1 / racine(s²)/racine(N)
Epsilon1 = 61-60 / racine(448)/(racine36)
Epsilon1 = 0,283
Pour Epsilon = 0,283, on trouve alpha = 78%.
De cette manière alpha1 / 2 = 39%
Probabilité de se trouver au dessus :
Epsilon2 = e2 / racine(s²)/racine(N)
Epsilon2 = 65-60 / racine(448)/(racine36)
Epsilon1 = 0,134
Pour Epsilon = 0,134, on trouve alpha = 26%.
De cette manière alpha2 / 2 = 39%
Pour trouver la probabilité se trouver en dedans de l'intervalle, entre 60 et 61 est donc : 0,5 (=ensemble des valeurs situées à gauche de la moyenne) - 0,39
Donc, 0,5 - 0,39 = 0,11
Pour trouver la probabilité se trouver en dedans de l'intervalle, entre 60 et 65 est donc : 0,5 (=ensemble des valeurs situées à droite de la moyenne) - 0,13
Donc, 0,5 - 0,13 = 0,37
En cumulant ces probabilités, pour un échantillon de 36 personnes, la probabilité d'observer une moyenne située entre 60 et 65 est donc : 11% + 37% = 48%
Etant donné que l'on travaille avec une moyenne, il est nécessaire d'utiliser les valeurs qui lui sont associées.
Ici, on n'utilise pas simplement la valeur de l'écart-type s mais la valeur de l'écart-type de la moyenne s/racine(N).
Ci-joint une réponse donnée auparavant qui explique la distinction entre ces deux écart-types pour mieux comprendre :
https://talc.forumgratuit.org/t10547-ecart-type-de-la-moyenne?highlight=moyenne
Pour résoudre cet exercice, on utilise la table de l'écart-réduit, qui nous permet de trouver le pourcentage que l'on recherche.
La particularité de la table de l'écart-réduit, c'est qu'elle ne nous permet pas de trouver la probabilité de se situer dans un pourcentage mais la probabilité de s'en trouver en dehors.
De plus, selon une répartition normale, la répartition des valeurs de l'échantillon étudié est symétrique de part et d'autre de la moyenne.
Cela signifie que l'on trouve 50% des valeurs à gauche de la moyenne et 50% des valeurs à droite de la moyenne.
Cependant, l'intervalle que l'on recherche n'est pas établit symétriquement par rapport à la moyenne (61).
On devra donc procéder par 2 étapes pour aboutir au résultat.
Un schéma peut nous aider à visualiser la situation :

On recherche donc la probabilité de se situer en dessous de l'intervalle (alpha1 / 2) et la probabilité de se situer au-dessus de l'intervalle (alpha2 / 2).
On recherche les valeurs de alpha grâce aux valeurs d'Epsilon :
Probabilité de se trouver en dessous :
Epsilon1 = e1 / racine(s²)/racine(N)
Epsilon1 = 61-60 / racine(448)/(racine36)
Epsilon1 = 0,283
Pour Epsilon = 0,283, on trouve alpha = 78%.
De cette manière alpha1 / 2 = 39%
Probabilité de se trouver au dessus :
Epsilon2 = e2 / racine(s²)/racine(N)
Epsilon2 = 65-60 / racine(448)/(racine36)
Epsilon1 = 0,134
Pour Epsilon = 0,134, on trouve alpha = 26%.
De cette manière alpha2 / 2 = 39%
Pour trouver la probabilité se trouver en dedans de l'intervalle, entre 60 et 61 est donc : 0,5 (=ensemble des valeurs situées à gauche de la moyenne) - 0,39
Donc, 0,5 - 0,39 = 0,11
Pour trouver la probabilité se trouver en dedans de l'intervalle, entre 60 et 65 est donc : 0,5 (=ensemble des valeurs situées à droite de la moyenne) - 0,13
Donc, 0,5 - 0,13 = 0,37
En cumulant ces probabilités, pour un échantillon de 36 personnes, la probabilité d'observer une moyenne située entre 60 et 65 est donc : 11% + 37% = 48%
Vault- Messages : 132
Date d'inscription : 20/09/2018
Marwa aime ce message
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
3) Détail du calcul pour le Test du Student :
- Nos effectifs sont inférieurs à 30
- La distribution gaussienne dans les population dont sont issus les échantillons est respectée
- Après le test de Fischer, on conclue à l'homogénéité de nos variances.
On calcule donc une variance commune Sc² :

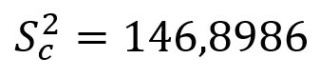
On introduit cette variance dans le calcul de notre t :

On compare cette valeur à la valeur théorique trouvée dans la Table de Student à DDL = Na - 1 + Nb -1 (donc 25) et pour alpha=5%
On trouve t théorique = 2,06
Comme t < t théorique, on ne rejette pas notre hypothèse nulle.
Il n'y a pas de différence significative entre les notes des QCM des étudiants issus des facultés A et C.
- Nos effectifs sont inférieurs à 30
- La distribution gaussienne dans les population dont sont issus les échantillons est respectée
- Après le test de Fischer, on conclue à l'homogénéité de nos variances.
On calcule donc une variance commune Sc² :

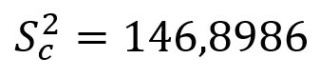
On introduit cette variance dans le calcul de notre t :

On compare cette valeur à la valeur théorique trouvée dans la Table de Student à DDL = Na - 1 + Nb -1 (donc 25) et pour alpha=5%
On trouve t théorique = 2,06
Comme t < t théorique, on ne rejette pas notre hypothèse nulle.
Il n'y a pas de différence significative entre les notes des QCM des étudiants issus des facultés A et C.
Vault- Messages : 132
Date d'inscription : 20/09/2018
Marwa aime ce message
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
4) Pour ta dernière question, je ne peux pas te refaire toute la démarche mais peux-tu me dire où tu bloques exactement ?
Vault- Messages : 132
Date d'inscription : 20/09/2018
 Re: ED 3 Ex 1 ex 2 et ex3
Re: ED 3 Ex 1 ex 2 et ex3
Merci infiniment pour toutes tes réponses !
Ne t'en fais pas pour la dernière j'ai su me débrouiller.
Merci x100000
Ne t'en fais pas pour la dernière j'ai su me débrouiller.
Merci x100000
Marwa- Messages : 12
Date d'inscription : 30/11/2020
Vault aime ce message
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum