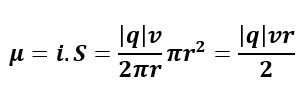Moment magnétique orbital
2 participants
Page 1 sur 1
 Moment magnétique orbital
Moment magnétique orbital
Bonsoir, je suis un peu perdue avec le moment magnétique orbital, je ne comprends pas a quoi il sert ni comment le calculer dans le cours le prof nous a donné plusieurs formulé mais, je n’arrive pas a comprendre comment on peut les appliquer et pourquoi cela reviendrait à la même chose entre mu= S x I et la formule avec h barre.
De plus je ne comprends pas dans quel cas on doit utiliser n, l, ml…
et enfin je ne comprends pas ce que signifie mu, mu z, mu e, et mu p …. Je vous mets mon cours parce que je ne pense pas être tres claire.
Ça serait super, si vous pouviez un peu m’éclairer,
Merci beaucoup

De plus je ne comprends pas dans quel cas on doit utiliser n, l, ml…
et enfin je ne comprends pas ce que signifie mu, mu z, mu e, et mu p …. Je vous mets mon cours parce que je ne pense pas être tres claire.
Ça serait super, si vous pouviez un peu m’éclairer,
Merci beaucoup

Clo.2108- Messages : 220
Date d'inscription : 02/10/2022
 Re: Moment magnétique orbital
Re: Moment magnétique orbital
Hey 
Le moment magnétique est un vecteur qui permet de caractériser l'intensité d'une source magnétique. Dans le cas d'une spire, le moment magnétique crée en son centre a pour :
- direction : perpendiculaire au plan de la spire
- sens : il forme un trièdre direct avec (dl; r ;M), il provient du produit vectoriel dlΛr (règle des 3 doigts de la main droite)
- norme : M = S.I avec S la surface en m (πr2)
Le moment magnétique sera très utile pour comprendre les phénomènes de résonnance magnétique dans le cas de l'IRM, même si la notion en soit reste un peu obscure.
Maintenant pour le cas du moment magnétique orbital(μ), c'est le même principe que la spire sauf qu'au lieu d'avoir une multitude de particules qui circulent, il n'y a plus qu'une particule qui tourne en orbite et créant ainsi un moment magnétique au centre de l'orbite. On peut detaillé un peu plus sa norme :
Mais il faut savoir que dans l'infiniment petit, dans le cas d'un éléctron notamment, tout est quantifié : le moment magnétique orbital ne peut pas prendre n'importe quelle valeur. Dans le cas de l'electron, il faut noter que :
- on peut calculer ce moment magnétique orbital quantifié en utilisant le magnéton de Bohr
- les valeurs du moment magnétique orbital qui peuvent être créées par un électron en orbite autour d’un noyau dépend de la valeur de l : le deuxième nombre quantique
Ce qui va être également quantifié c’est l’orientation de la trajectoire de l'electron. En effet, elle ne peut pas prendre toutes les orientations possibles. Pour cela on va pouvoir calculer μz qui est la composante verticale du moment magnétique orbitale. Sa norme dépend cette fois du 3eme nombre quantique:
Je te mets un exemple de cette application :
Bon courage
Le moment magnétique est un vecteur qui permet de caractériser l'intensité d'une source magnétique. Dans le cas d'une spire, le moment magnétique crée en son centre a pour :
- direction : perpendiculaire au plan de la spire
- sens : il forme un trièdre direct avec (dl; r ;M), il provient du produit vectoriel dlΛr (règle des 3 doigts de la main droite)
- norme : M = S.I avec S la surface en m (πr2)
Le moment magnétique sera très utile pour comprendre les phénomènes de résonnance magnétique dans le cas de l'IRM, même si la notion en soit reste un peu obscure.
Maintenant pour le cas du moment magnétique orbital(μ), c'est le même principe que la spire sauf qu'au lieu d'avoir une multitude de particules qui circulent, il n'y a plus qu'une particule qui tourne en orbite et créant ainsi un moment magnétique au centre de l'orbite. On peut detaillé un peu plus sa norme :
Mais il faut savoir que dans l'infiniment petit, dans le cas d'un éléctron notamment, tout est quantifié : le moment magnétique orbital ne peut pas prendre n'importe quelle valeur. Dans le cas de l'electron, il faut noter que :
- on peut calculer ce moment magnétique orbital quantifié en utilisant le magnéton de Bohr
- les valeurs du moment magnétique orbital qui peuvent être créées par un électron en orbite autour d’un noyau dépend de la valeur de l : le deuxième nombre quantique
Ce qui va être également quantifié c’est l’orientation de la trajectoire de l'electron. En effet, elle ne peut pas prendre toutes les orientations possibles. Pour cela on va pouvoir calculer μz qui est la composante verticale du moment magnétique orbitale. Sa norme dépend cette fois du 3eme nombre quantique:
Je te mets un exemple de cette application :
Bon courage

Clembrdy- Messages : 125
Date d'inscription : 07/12/2021
Age : 21
 Re: Moment magnétique orbital
Re: Moment magnétique orbital
Super merci beaucoup ! Mais ducoup pour caractériser mon moment magnétique orbital je dois faire les deux calculs l’un avec mu = q x v x r /2 et l’autre avec le nombre quantique ou bien les deux reviennent a la même chose ?
Et aussi je n’arrive pas à trouver a quoi correspond mu e et mu p qui sont des constantes ?
Et aussi je n’arrive pas à trouver a quoi correspond mu e et mu p qui sont des constantes ?
Clo.2108- Messages : 220
Date d'inscription : 02/10/2022
 Re: Moment magnétique orbital
Re: Moment magnétique orbital
Les deux vont revenir à la même chose ! Après tu n'utilisera jamais ça en exercice 
Dans ton cours μe et μp sont respectivement le magneton de Bohr pour l'électron et le proton, leur valeur n'est pas à connaitre.
Bon courage
Dans ton cours μe et μp sont respectivement le magneton de Bohr pour l'électron et le proton, leur valeur n'est pas à connaitre.
Bon courage

Clembrdy- Messages : 125
Date d'inscription : 07/12/2021
Age : 21
Clo.2108 aime ce message
 Sujets similaires
Sujets similaires» Moment magnétique orbital
» Moment magnétique et moment cinétique
» Moment Magnétique
» Moment Magnétique
» moment magnétique, magnéton
» Moment magnétique et moment cinétique
» Moment Magnétique
» Moment Magnétique
» moment magnétique, magnéton
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum