QCM 11 mai 2016

Hello ! Pour ce QCM je trouve la réponse c), qu'en pensez-vous ?

Merci d'avance

C'est exact

Bonjour j'aimerai bien savoir comment faites vous pour trouver ça parce que j'ai un résultat très proche

Bonjour,

Pour le segment d'artériole, la résistance est de 8ηL/πR^4 = 8ηL/16πr^4 car R=2r donc R^4=16r^4 On obtient alors 1/2. ηL/πr^4

Pour la résistance équivalente des capillaires, 1/Réq = 16 x 1/R(1capillaire) car les 16 capillaires sont disposés en dérivation, ce qui donne 1/Réq = 16 x πr^4/8ηL = 2πr^4/ηL
On a alors en inversant Réq=1/2. ηL/πr^4

En faisant la somme des deux, on a Rglobale = 1/2. ηL/πr^4 + 1/2. ηL/πr^4 = ηL/πr^4 (réponse C)

Salut salut !!

Je voulais savoir si il était possible de faire simplement ce calcul, puisqu'au final je trouve le même résultat ?

Merci beaucoup

Explique un peu à quoi correspondent tes variables et ton raisonnement. :/

J'ai divisé par 16 puisque l'artériole est divisée en 16 capillaires
Ensuite, comme chaque capillaire à un rayon r égal à la moitié de celui de l'artériole, j'ai donc multiplié ce r par 1/2

Sauf que plus haut, dans une de tes réponses, tu utilise la dérivation. Donc je voulais savoir si ma façon de raisonner revenait à la même chose ?!

Merci bcp

Je crois que tu as oublié de changer ton r en passant du rayon capillaire au rayon artériolaire (r=1/2.R)
Si je suis ta méthode on se retrouve avec une résistance en fonction de R.

En fait tu as juste calculer la résistance globale des 16 capillaire. Et celle-ci est correcte mais tu l'as exprimé avec le mauvais rayon.
Tu dois aussi lui additionner la résistance du bout d'artériole pour avoir la résistance de l'ensemble.

Donc je trouve le bon résultat mais par chance ?!

Non en fait tu as fait que la 1/2 de l'exercice. Et ton résultat n'est pas bon. Tu as écrit r alors que c'est R

Pourquoi 1/Réq = 16 x πr^4/8ηL = 2πr^4/ηL ? Je veux dire pourquoi est-on obligé de prendre l'inverse de la résistance?
pourquoi pas simplement: Re = 16. re? C'est une règle de physique ?

Pour un circuit en dérivation, oui c'est obligatoire
1/Req = Somme des 1/Ri

Je me permet je relancer le sujet car je ne comprend pas pourquoi il faut faire l'inverse de la résistance des capillaires?
Car sans faire l'inverse on se retrouve avec 8*16 au numérateur donc impossible de trouver le bon résultat mais en même temps je ne comprend pas pourquoi il faut faire l'inverse...
Car lorsque que l'on fait l'inverse dans le corrigé du talc nous avons : 1/Req = 16 * 1/w (résistance 1 capi)...
Je ne comprend pas pourquoi on met 16 et pas 1/16 également ...

Merci d'avance

Bonjour, je ne comprends pas à quoi correspond dans le début de la résolution de l'exercice l'égalité suivante : 1 / Réq = 16 * 1/ω'

Serait-il possible d'avoir une explication s'il vous plait?
Je vous remercie

Bonsoir !

Dans cet exercice, les 16 capillaires sont en dérivation. D'après le cours de Cavillon, tu dois utiliser cette formule :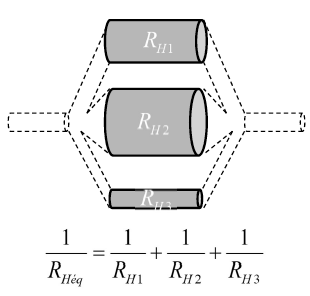
Ici, les 16 capillaires sont identiques donc ils ont la même résistance : tu additionnes donc 16 fois le même quotient (1/ω'). Avec une factorisation, tu obtiens l'égalité à droite sur la première ligne.

Bon courage !

danke schön !

Salut !

Peux tu nous envoyer ton brouillon merci !

Bon courage
L'ours

Salut !
Je viens de m'apercevoir que personne ne t'avait répondu... J'espère ne pas arriver après la bataille... :'(
Ligne 2 : pour le calcul de la résistance des capillaires, tu as mis un rayon égal à r/2 alors qu'il est dit que le capillaire a un rayon de r seulement (ou R/2)

Encore désolée et beaucoup de courage pour le reste à venir !