loi de jurin et capillarité

heyyy,

En fait je comprends pas trop les différentes situations de la loi de Laplace:
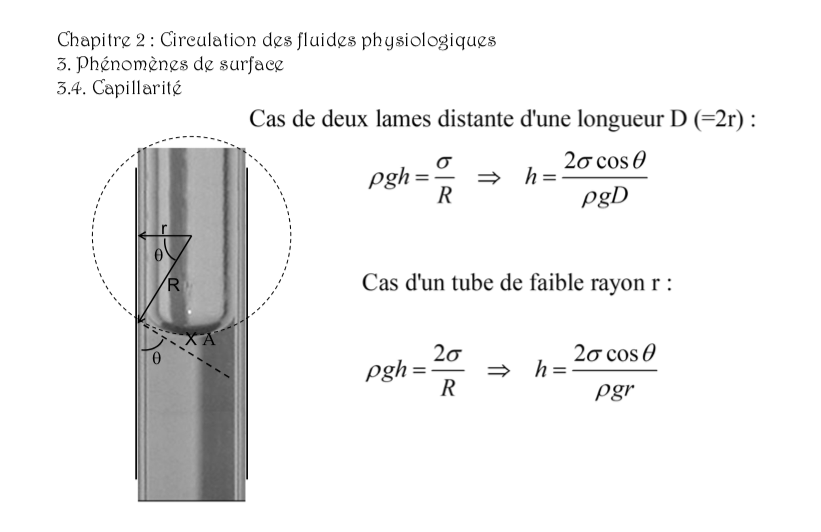
- parce qu'on dit que dans le cas d'un cylindre la loi de Laplace c'est Pi - Pe = sigma / r
- dans le cas d'une goutte : Pi-Pe = 2 sigma / r
- dans le cas d'une double membrane : Pi - Pe = 4 sigma / r

et donc je vois pas pourquoi on dit sur ce slide du chapitre 3 que
- dans le cas d'un faible diamètre : pgh = 2sigma/R
- alors que dans le cas d'où les deux lames sont distante d'une longueur D: pgh = sigma/R.
J'ai compris que la loi de Jurin c'est quand on considère que loi de l'hydrostatique et la loi de Laplace s'applique, mais je ne comprends pas pq 2 sigma et puis sigma....



Merci d'avance (j'espère que ma question était claire)

Hello !

Alors en gros dans le cas de 2 lames rapprochées, l'interface air-liquide s'apparente à la partie inférieure d'un cylindre d'où le sigma/R.
Tandis que dans le cas d'un tube avec un diamètre assez petit pour qu'il y ait capillarité, l'interface air-liquide s'apparente à la partie inférieure d'une sphère (donc comme une goutte) d'où le 2sigma/R.

C'est good ou t'es toujours dans le flou ?

nonnn merci beaucoup!!!

auvray a écrit:Hello !

Alors en gros dans le cas de 2 lames rapprochées, l'interface air-liquide s'apparente à la partie inférieure d'un cylindre d'où le sigma/R.
Tandis que dans le cas d'un tube avec un diamètre assez petit pour qu'il y ait capillarité, l'interface air-liquide s'apparente à la partie inférieure d'une sphère (donc  comme une goutte) d'où le 2sigma/R.

je suis dans le flou perso

Salut !
Réponse tardive, il faut pas hésiter à relancer si jamais tu as besoin
Encore désolée...

Quand tu rapproches deux lames l'une de l'autre, tu te retrouveras avec une partie de cylindre entre les deux, car une des parties n'est pas fermée
Il n'y a donc pas de ménisque aux endroits où il n'y a pas de lame.
Dans le cas d'un cylindre, tu prends une différence de pression = sigma/r
Je te mets un petit schéma pour que tu comprennes un peu mieux


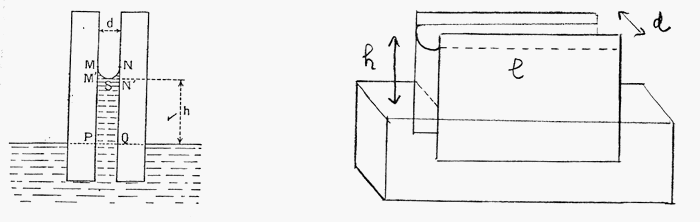
A contrario, dans le cas d'un tube, tous les côtés sont fermés. Le ménisque va donc s'étendre sur toute la paroi du tube. Ainsi, comme montré sur le schéma du premier message, l'interface s'apparente à la partie inférieure d'une sphère.
Tu vas donc donner une différence de pression qui est 2sigma/r

C'est un peu mieux ?