ED1 stat 2018
2 participants
Page 1 sur 1
 ED1 stat 2018
ED1 stat 2018
Bonjour ,
je n'arrive pas à comprendre une étape, dans le correction de la dernière question de l'exo 1 de l'ED 2018.
En fait je n'arrive pas à comprendre comment on conclut que la proba d'être sup à 29 est de 0,5% et que le proba d'être inférieur à 16 est 0,305%...
(je remets l'énoncé ainsi que la correction de la question)
Merci pour votre aide !
Exercice I : Un certain nombre d’études ont été menées afin de savoir si l’homéopathie à un effet au-delà de l’effet
placebo. On réalise une méta-analyse, c’est-à-dire qu’on va recueillir et étudier l’ensemble des articles scientifiques
publiés sur le sujet. On recense 300 articles exploitables sur le sujet, toutes les études ont été menées en fixant le
risque de première espèce à 5%.
18 articles concluent à une différence entre l’homéopathie et le placebo. Les autres ne retrouvent pas de différence
d’efficacité entre le traitement homéopathique et le placebo.
La méta-analyse permet de calculer l’Odds-ratio global à toutes ces études qui est de 0.88 IC95%[0,65 ;1,19] avec une
significativité p=0,30
5) Quelle est la probabilité d’observer entre 16 et 29 articles concluant à une différence entre homéopathie et
placebo
correction =
P = 18/300 soit 0,06 et s= rac(0,06 * 0.94/300) = 0,0137
Pour 29/300 p = 0,096 et e= 0,096 – 0,06 = 0,036 ɛ=0,036/0,0137 = 2,62 soit 0,01
La probabilité d’être sup à 29 = 0,5%
Pour 16/30 p = 0,053 et e = 0,007 ɛ=0,007/0,0137 = 0,51 soit 0,61
La probabilité d’être inf à 16 = 0,305
La probabilité d’observer entre 16 et 29 articles est de 1- 0,305 – 0,005 = 69%
je n'arrive pas à comprendre une étape, dans le correction de la dernière question de l'exo 1 de l'ED 2018.
En fait je n'arrive pas à comprendre comment on conclut que la proba d'être sup à 29 est de 0,5% et que le proba d'être inférieur à 16 est 0,305%...
(je remets l'énoncé ainsi que la correction de la question)
Merci pour votre aide !
Exercice I : Un certain nombre d’études ont été menées afin de savoir si l’homéopathie à un effet au-delà de l’effet
placebo. On réalise une méta-analyse, c’est-à-dire qu’on va recueillir et étudier l’ensemble des articles scientifiques
publiés sur le sujet. On recense 300 articles exploitables sur le sujet, toutes les études ont été menées en fixant le
risque de première espèce à 5%.
18 articles concluent à une différence entre l’homéopathie et le placebo. Les autres ne retrouvent pas de différence
d’efficacité entre le traitement homéopathique et le placebo.
La méta-analyse permet de calculer l’Odds-ratio global à toutes ces études qui est de 0.88 IC95%[0,65 ;1,19] avec une
significativité p=0,30
5) Quelle est la probabilité d’observer entre 16 et 29 articles concluant à une différence entre homéopathie et
placebo
correction =
P = 18/300 soit 0,06 et s= rac(0,06 * 0.94/300) = 0,0137
Pour 29/300 p = 0,096 et e= 0,096 – 0,06 = 0,036 ɛ=0,036/0,0137 = 2,62 soit 0,01
La probabilité d’être sup à 29 = 0,5%
Pour 16/30 p = 0,053 et e = 0,007 ɛ=0,007/0,0137 = 0,51 soit 0,61
La probabilité d’être inf à 16 = 0,305
La probabilité d’observer entre 16 et 29 articles est de 1- 0,305 – 0,005 = 69%
mamath- Messages : 15
Date d'inscription : 17/09/2020
Age : 22
 Re: ED1 stat 2018
Re: ED1 stat 2018
Bonjour,
Reprenons l'ensemble de l'exercice!
On obtient à partir de l'énoncé les informations suivantes :
Attention à ne pas confondre p et q ; ici on s'interroge sur le nombre d'articles concluant à une différence en homéopathie et placébo, qui vaut donc bien p.
On peut calculer notre écart-type: s = racine( p*q / n ) = racine( 0,06*0,94 / 300 ) = 0,0137
Abordons la question : "Quelle est la probabilité d’observer entre 16 et 29 articles concluant à une différence entre homéopathie et
placebo?"
Comme nous travaillons avec des données qualitatives, il faut impérativement exprimer ces nombres sous forme de proportions.
Ainsi, on utilise 16/300 = 0,053 et 29/300 = 0,097.
On remarque que notre proportion p = 0,06 se situe entre ces deux bornes - ce n'est pas une coïncidence.
Calculons désormais les écarts. Nous sommes obligés d'en calculer deux, car ils ne sont pas de la même grandeur (autrement dit : 0,06 est compris entre 0,053 et 0,097 mais ne se situe pas pile au milieu de ces deux bornes).
e1 = 0,06 — 0,053 = 0,007
e2 = 0,097 — 0,06 = 0,037
Nous obtenons la représentation suivante :
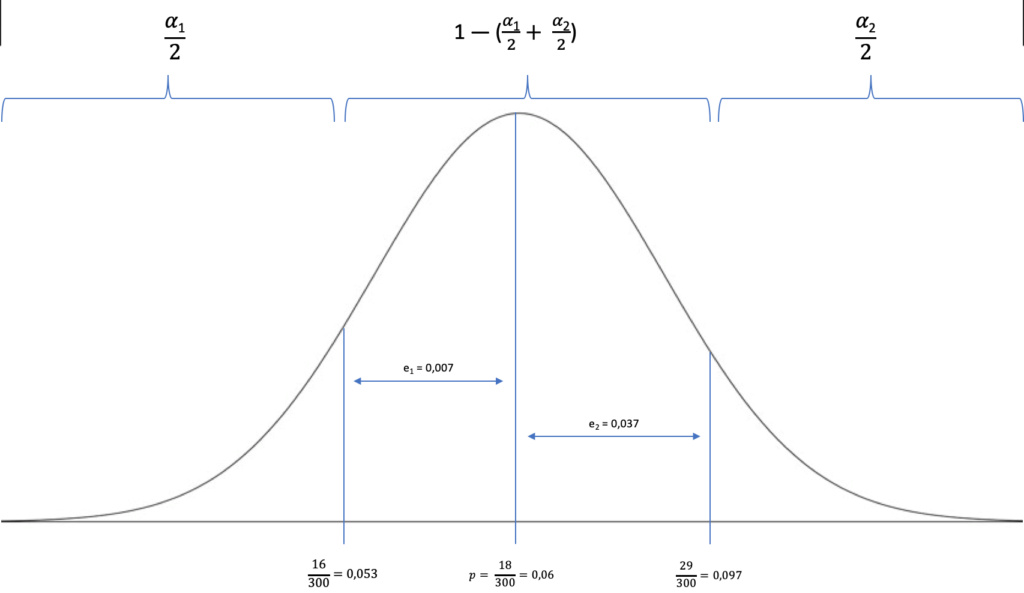
Nous pouvons calculer les écarts réduits "epsilon" ; comme il y a deux écarts e, il y a forcément deux écarts réduits.
epsilon1 = e1 / s = 0,007 / 0,0137 = 0,51
epsilon2 = e2 / s = 0,037 / 0,0137 = 2,7
Avec ces valeurs fraîchement calculées, nous pouvons trouver les valeurs d'alpha associées en utilisant la table de l'écart réduit :
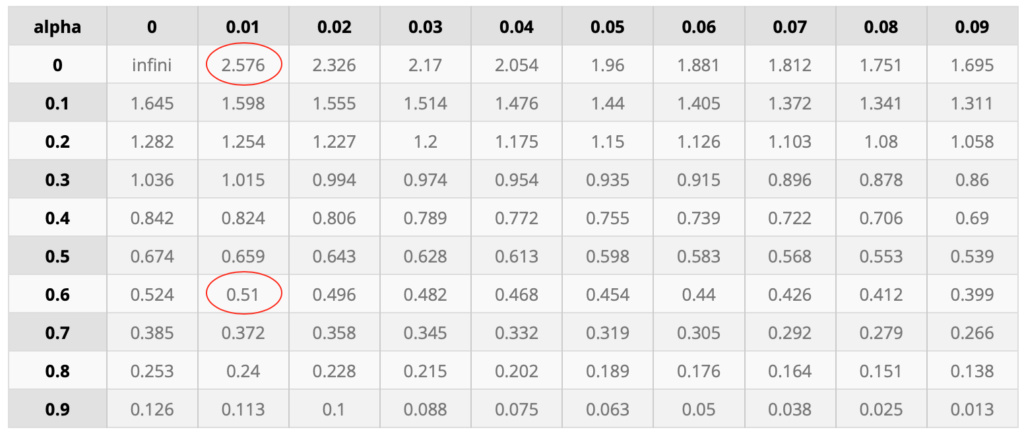
On trouve :
alpha1 = 0,61
alpha2 = 0,01
Passons à l'interprétation.
La valeur alpha désigne les zones en dehors de l'intervalle de confiance (on parle de zones au pluriel car il y a une zone plus grande et une zone plus petite).
La valeur 1 — alpha désigne la zone en dedans de l'intervalle de confiance.
C'est ce que j'ai représenté en haut de la première image.
Il faut diviser nos valeurs d'alpha par 2 afin qu'elles ne représentent chacune qu'une moitié de la zone en dehors de l'intervalle de confiance.
alpha1 / 2 correspond à la zone plus petite que l'intervalle de confiance ---> alpha1 / 2 = 0,61 / 2 = 0,305 soit 30,5%
alpha2 / 2 correspond à la zone plus grande que l'intervalle de confiance ---> alpha2 / 2 = 0,01 / 2 = 0,005 soit 0,5%
La question nous demande la probabilité de se situer en dedans de l'intervalle de confiance, soit 1 — alpha.
On a : 1 — alpha = 1 — [ (alpha1 / 2) + (alpha2 / 2)] = 1 — [0,305 + 0,005] = 1 — 0,31 = 0,69 soit 69%.
Au final, la probabilité
Ce sont des notions assez difficiles à aborder la première fois, mais absolument essentielles. N'hésite pas à te manifester si tu as encore des questions.
Bon courage!
Reprenons l'ensemble de l'exercice!
On obtient à partir de l'énoncé les informations suivantes :
- n = 300
- alpha = 5% = 0,05
- p = 18/300 = 6% = 0,06
- q = 282/300 = 94% = 0,94
Attention à ne pas confondre p et q ; ici on s'interroge sur le nombre d'articles concluant à une différence en homéopathie et placébo, qui vaut donc bien p.
On peut calculer notre écart-type: s = racine( p*q / n ) = racine( 0,06*0,94 / 300 ) = 0,0137
Abordons la question : "Quelle est la probabilité d’observer entre 16 et 29 articles concluant à une différence entre homéopathie et
placebo?"
Comme nous travaillons avec des données qualitatives, il faut impérativement exprimer ces nombres sous forme de proportions.
Ainsi, on utilise 16/300 = 0,053 et 29/300 = 0,097.
On remarque que notre proportion p = 0,06 se situe entre ces deux bornes - ce n'est pas une coïncidence.
Calculons désormais les écarts. Nous sommes obligés d'en calculer deux, car ils ne sont pas de la même grandeur (autrement dit : 0,06 est compris entre 0,053 et 0,097 mais ne se situe pas pile au milieu de ces deux bornes).
e1 = 0,06 — 0,053 = 0,007
e2 = 0,097 — 0,06 = 0,037
Nous obtenons la représentation suivante :

Nous pouvons calculer les écarts réduits "epsilon" ; comme il y a deux écarts e, il y a forcément deux écarts réduits.
epsilon1 = e1 / s = 0,007 / 0,0137 = 0,51
epsilon2 = e2 / s = 0,037 / 0,0137 = 2,7
Avec ces valeurs fraîchement calculées, nous pouvons trouver les valeurs d'alpha associées en utilisant la table de l'écart réduit :

On trouve :
alpha1 = 0,61
alpha2 = 0,01
Passons à l'interprétation.
La valeur alpha désigne les zones en dehors de l'intervalle de confiance (on parle de zones au pluriel car il y a une zone plus grande et une zone plus petite).
La valeur 1 — alpha désigne la zone en dedans de l'intervalle de confiance.
C'est ce que j'ai représenté en haut de la première image.
Il faut diviser nos valeurs d'alpha par 2 afin qu'elles ne représentent chacune qu'une moitié de la zone en dehors de l'intervalle de confiance.
alpha1 / 2 correspond à la zone plus petite que l'intervalle de confiance ---> alpha1 / 2 = 0,61 / 2 = 0,305 soit 30,5%
alpha2 / 2 correspond à la zone plus grande que l'intervalle de confiance ---> alpha2 / 2 = 0,01 / 2 = 0,005 soit 0,5%
La question nous demande la probabilité de se situer en dedans de l'intervalle de confiance, soit 1 — alpha.
On a : 1 — alpha = 1 — [ (alpha1 / 2) + (alpha2 / 2)] = 1 — [0,305 + 0,005] = 1 — 0,31 = 0,69 soit 69%.
Au final, la probabilité
- d'observer moins de 16 articles concluant à une différence entre homéopathie et placébo est de 30,5%
- d'observer entre 16 et 29 articles concluant à une différence entre homéopathie et placébo est de 69%
- d'observer plus de 29 articles concluant à une différence entre homéopathie et placébo est de 0,5%
Ce sont des notions assez difficiles à aborder la première fois, mais absolument essentielles. N'hésite pas à te manifester si tu as encore des questions.
Bon courage!

Dawson- Messages : 17
Date d'inscription : 23/02/2020
Age : 24
mamath aime ce message
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum