ED 2020-2021
5 participants
Tutorat Licence Santé Lille Catho :: L1 - Chimie, Chimie Organique, Chimie Structurale, Génétique et Biochimie :: Questions de cours et d'ED :: BIOCHIMIE
Page 1 sur 1
 ED 2020-2021
ED 2020-2021
Bonjour j’ai une petite question au sujet de l’ed d’enzymo de cette année.
Voilà pour l’exercice 1 (question 2) je ne vois pas bien comment calculer le Ki et même chose pour l’exercice 4 (question 4). Je pense que c’est la même méthode mais je ne vois pas laquelle...
est ce que quelqu’un pourrait m’aider ?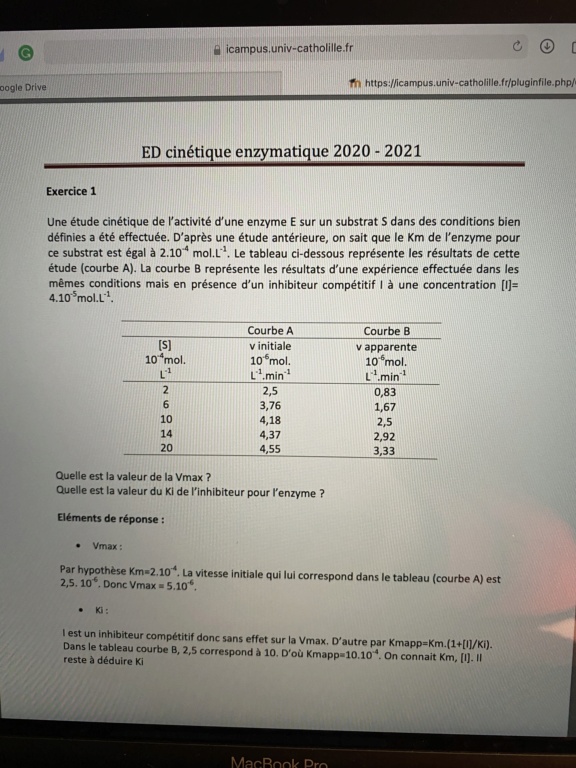

Voilà pour l’exercice 1 (question 2) je ne vois pas bien comment calculer le Ki et même chose pour l’exercice 4 (question 4). Je pense que c’est la même méthode mais je ne vois pas laquelle...
est ce que quelqu’un pourrait m’aider ?



Dr Juiphe- Messages : 210
Date d'inscription : 02/11/2020
Age : 22
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !
Exercice 1 :
On te dit que l’inhibiteur ajouté au milieu est de type compétitif, ce qui signifie que le Km sera modifié d’un facteur (1 + [I]/Ki)
Donc Kmapp = Km × (1 + [I]/Ki)
Il te faut donc isoler Ki :
Kmapp / Km = 1 + [I]/Ki
Kmapp / Km – 1 = [I]/Ki
(Kmapp – Km) / Km = [I]/Ki
Km / (Kmapp – Km) = Ki/[I]
Ki = (Km × [I]) / (Kmapp – Km)
Ensuite tu remplaces, sachant que Km et [I] sont donnés dans l’énoncé.
Finalement, il restera à déterminer la valeur de Kmapp, et pour cela on utilisera le tableau.
Dans le cours, on définit Km comme étant la quantité de substrat pour laquelle la vitesse initiale est égale à la moitié de la vitesse maximale, ce qui revient à dire que si Km = [S], alors V0 = Vmax/2
Donc dans notre tableau, on regarde la colonne [S], et on choisit la ligne correspondant à [S] = Km, donc ici à [S] = 2.10⁻4
Sur cette ligne, on voit que la V0 correspondante est de 2,5.10-6, donc Vmax = 2 × 2,5.10-6 = 5.10-6
Comme il s’agit d’un inhibiteur compétitif, la Vmax est identique avec ou sans inhibiteur.
Donc dans la colonne de la courbe B (V apparente), on retrouve la V0 correspondante, qui était de 2,5.10-6. Ensuite, on regarde la [S] correspondante, qui est de 10.10-4 et comme [S] = Km si V0 = Vmax/2, on a Kmapp = [S]app = 10.10-4
Il ne te reste plus qu’à faire le calcul !
Exercice 4 :
Ici pour déterminer la valeur du Km, il faut savoir de quel type d’inhibition il s’agit.
Je te renvoie ici pour avoir le détail du procédé : https://talc.forumgratuit.org/t11293-representation-graphique-cinetique-enzymatique
On sait donc qu’il s’agit d’un inhibiteur incompétitif, donc diminution de Km et Vmax d’un même facteur (1 + [I]/Ki)
Donc Kmapp = Km / (1 + [I]/Ki)
Kmapp × (1 + [I]/Ki) = Km
Kmapp + (Kmapp × [I]) / Ki = Km
(Kmapp × [I]) / Ki = Km – Kmapp
1/Ki = (Km – Kmapp) / (Kmapp × [I])
Ki = (Kmapp × [I]) / (Km – Kmapp)
Avec Km calculé dans les questions précédentes, [I] donné dans l’énoncé et Kmapp qui correspond au Km de la courbe B.
Voilà, j'espère que c'est plus clair pour toi
Exercice 1 :
On te dit que l’inhibiteur ajouté au milieu est de type compétitif, ce qui signifie que le Km sera modifié d’un facteur (1 + [I]/Ki)
Donc Kmapp = Km × (1 + [I]/Ki)
Il te faut donc isoler Ki :
Kmapp / Km = 1 + [I]/Ki
Kmapp / Km – 1 = [I]/Ki
(Kmapp – Km) / Km = [I]/Ki
Km / (Kmapp – Km) = Ki/[I]
Ki = (Km × [I]) / (Kmapp – Km)
Ensuite tu remplaces, sachant que Km et [I] sont donnés dans l’énoncé.
Finalement, il restera à déterminer la valeur de Kmapp, et pour cela on utilisera le tableau.
Dans le cours, on définit Km comme étant la quantité de substrat pour laquelle la vitesse initiale est égale à la moitié de la vitesse maximale, ce qui revient à dire que si Km = [S], alors V0 = Vmax/2
Donc dans notre tableau, on regarde la colonne [S], et on choisit la ligne correspondant à [S] = Km, donc ici à [S] = 2.10⁻4
Sur cette ligne, on voit que la V0 correspondante est de 2,5.10-6, donc Vmax = 2 × 2,5.10-6 = 5.10-6
Comme il s’agit d’un inhibiteur compétitif, la Vmax est identique avec ou sans inhibiteur.
Donc dans la colonne de la courbe B (V apparente), on retrouve la V0 correspondante, qui était de 2,5.10-6. Ensuite, on regarde la [S] correspondante, qui est de 10.10-4 et comme [S] = Km si V0 = Vmax/2, on a Kmapp = [S]app = 10.10-4
Il ne te reste plus qu’à faire le calcul !
Exercice 4 :
Ici pour déterminer la valeur du Km, il faut savoir de quel type d’inhibition il s’agit.
Je te renvoie ici pour avoir le détail du procédé : https://talc.forumgratuit.org/t11293-representation-graphique-cinetique-enzymatique
On sait donc qu’il s’agit d’un inhibiteur incompétitif, donc diminution de Km et Vmax d’un même facteur (1 + [I]/Ki)
Donc Kmapp = Km / (1 + [I]/Ki)
Kmapp × (1 + [I]/Ki) = Km
Kmapp + (Kmapp × [I]) / Ki = Km
(Kmapp × [I]) / Ki = Km – Kmapp
1/Ki = (Km – Kmapp) / (Kmapp × [I])
Ki = (Kmapp × [I]) / (Km – Kmapp)
Avec Km calculé dans les questions précédentes, [I] donné dans l’énoncé et Kmapp qui correspond au Km de la courbe B.
Voilà, j'espère que c'est plus clair pour toi

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
Dr Juiphe aime ce message
 Re: ED 2020-2021
Re: ED 2020-2021
Salut! Merci beaucoup pour la réponse super complète, j’ai bien compris pour l’exo 1 mais ça coince encore un peu pour l’exo 4 vraiment désolée  j’ai essayé de faire ça au brouillon mais je pense que mes calculs de la vmax (1ere question) et du km (2ème question) ne sont pas bons... et je ne comprends pas bien le graph en fait, comment on peut dire que c’est un inhibiteur incompetitif (les droites ne sont pas parallèles?), parce qu’il ressemble pas vraiment à ceux qu’on a l’habitude de voir, je visualise pas trop avec les valeurs en ordonné et abscisses...
j’ai essayé de faire ça au brouillon mais je pense que mes calculs de la vmax (1ere question) et du km (2ème question) ne sont pas bons... et je ne comprends pas bien le graph en fait, comment on peut dire que c’est un inhibiteur incompetitif (les droites ne sont pas parallèles?), parce qu’il ressemble pas vraiment à ceux qu’on a l’habitude de voir, je visualise pas trop avec les valeurs en ordonné et abscisses...

Dr Juiphe- Messages : 210
Date d'inscription : 02/11/2020
Age : 22
 Re: ED 2020-2021
Re: ED 2020-2021
Ok, on va tout reprendre tranquillement alors !
Quand tu retrouves face à un exo comme ça, la première chose à faire c'est de savoir quel est le contexte : est-ce que la représentation graphique est une représentation de Linewear et Burk ?
-> Si oui, alors tu peux appliquer les propriétés que tu connais (le cours donc)
-> Si non, il faut déterminer quelle représentation tu as
Ici, ce n'est pas une Linewear et Burk, donc il faut déterminer l'équation de la droite.
Tu n'auras toujours que des droites affines, donc le procédé est toujours le même !
Tu regardes les axes, et tu en déduis une partie de ton équation : ici, on a en abscisse V0/[S] (qui sera donc ton x) et en ordonnée V0 (qui sera donc ton y)
Ainsi, on a : y = ax + b qui devient V0 = a × (V0/[S]) + b
Il nous reste donc à en déduire a et b
Pour ce faire, tu pars toujours de la même formule, qui est vraiment la base de tout en enzymo : V0 = (Vmax × [S]) / (Km + [S])
Et tu dois bidouiller pour parvenir à retrouver les termes V0 et V0/[S] :
V0 = (Vmax × [S]) / (Km + [S])
V0 × (Km + [S]) = Vmax × [S]
V0/[S] × (Km + [S]) = Vmax
(V0 × Km)/[S] + (V0 × [S])/[S] = Vmax
(V0 × Km)/[S] + V0 = Vmax
V0 = Vmax - (V0 × Km)/[S]
V0 = Vmax - (V0/[S] × Km)
Soit : V0 = V0/[S] × (- Km) + Vmax
Par identification, tu trouves donc y = V0, x = V0/[S], a = - Km et b = Vmax
Graphiquement, ça va se traduire de la façon suivante :
Variation de Km = variation du coefficient directeur de la droite, c'est-à-dire variation de l'inclinaison de ta droite
Variation de Vmax = variation de l'ordonnée à l'origine de la droite, c'est-à-dire variation du point d'intersection entre la courbe et l'axe des ordonnées
Ici, à l'ajout de l'inhibiteur (courbe B), on a bien une variation du coefficient directeur ET de l'ordonnée à l'origine, donc variation de Km ET de Vmax, ce qui correspond à un inhibiteur incompétitif (uncompétitif, anti-compétitif).
Maintenant qu'on sait tout ça, c'est tout de suite beaucoup plus facile de s'occuper du reste !
On te demande de calculer Vmax, or Vmax correspond à l'ordonnée à l'origine : on peut donc la déduire graphiquement, la valeur de Vmax correspondant à la valeur retrouvée sur l'axe des ordonnées lorsqu'il est coupé par la courbe, soit ici 10.10⁻⁶ !
Pour calculer Km, on va choisir un point sur la courbe et on va résoudre l'équation de la droite
On choisit par exemple le point de coordonnées (10.10⁻² ; 0), parce qu'il est facile à lire
On remplace les valeurs de x et y dans l'équation de la droite :
V0 = V0/[S] × (- Km) + Vmax
0 = 10.10⁻² × (- Km) + Vmax
Sachant que Vmax = 10.10⁻⁶
0 = 10.10⁻² × (- Km) + 10.10⁻⁶
Il ne reste plus qu'à isoler Km !
0 = 10.10⁻² × (- Km) + 10.10⁻⁶
- 10.10⁻⁶ = 10.10⁻² × (- Km)
(- 10.10⁻⁶) / 10.10⁻² = - Km
Km = 10.10⁻⁶ / 10.10⁻²
Km = 10⁻⁴
Voilà, j'espère que c'est plus clair pour toi
Quand tu retrouves face à un exo comme ça, la première chose à faire c'est de savoir quel est le contexte : est-ce que la représentation graphique est une représentation de Linewear et Burk ?
-> Si oui, alors tu peux appliquer les propriétés que tu connais (le cours donc)
-> Si non, il faut déterminer quelle représentation tu as
Ici, ce n'est pas une Linewear et Burk, donc il faut déterminer l'équation de la droite.
Tu n'auras toujours que des droites affines, donc le procédé est toujours le même !
Tu regardes les axes, et tu en déduis une partie de ton équation : ici, on a en abscisse V0/[S] (qui sera donc ton x) et en ordonnée V0 (qui sera donc ton y)
Ainsi, on a : y = ax + b qui devient V0 = a × (V0/[S]) + b
Il nous reste donc à en déduire a et b
Pour ce faire, tu pars toujours de la même formule, qui est vraiment la base de tout en enzymo : V0 = (Vmax × [S]) / (Km + [S])
Et tu dois bidouiller pour parvenir à retrouver les termes V0 et V0/[S] :
V0 = (Vmax × [S]) / (Km + [S])
V0 × (Km + [S]) = Vmax × [S]
V0/[S] × (Km + [S]) = Vmax
(V0 × Km)/[S] + (V0 × [S])/[S] = Vmax
(V0 × Km)/[S] + V0 = Vmax
V0 = Vmax - (V0 × Km)/[S]
V0 = Vmax - (V0/[S] × Km)
Soit : V0 = V0/[S] × (- Km) + Vmax
Par identification, tu trouves donc y = V0, x = V0/[S], a = - Km et b = Vmax
Graphiquement, ça va se traduire de la façon suivante :
Variation de Km = variation du coefficient directeur de la droite, c'est-à-dire variation de l'inclinaison de ta droite
Variation de Vmax = variation de l'ordonnée à l'origine de la droite, c'est-à-dire variation du point d'intersection entre la courbe et l'axe des ordonnées
Ici, à l'ajout de l'inhibiteur (courbe B), on a bien une variation du coefficient directeur ET de l'ordonnée à l'origine, donc variation de Km ET de Vmax, ce qui correspond à un inhibiteur incompétitif (uncompétitif, anti-compétitif).
Maintenant qu'on sait tout ça, c'est tout de suite beaucoup plus facile de s'occuper du reste !
On te demande de calculer Vmax, or Vmax correspond à l'ordonnée à l'origine : on peut donc la déduire graphiquement, la valeur de Vmax correspondant à la valeur retrouvée sur l'axe des ordonnées lorsqu'il est coupé par la courbe, soit ici 10.10⁻⁶ !
Pour calculer Km, on va choisir un point sur la courbe et on va résoudre l'équation de la droite
On choisit par exemple le point de coordonnées (10.10⁻² ; 0), parce qu'il est facile à lire
On remplace les valeurs de x et y dans l'équation de la droite :
V0 = V0/[S] × (- Km) + Vmax
0 = 10.10⁻² × (- Km) + Vmax
Sachant que Vmax = 10.10⁻⁶
0 = 10.10⁻² × (- Km) + 10.10⁻⁶
Il ne reste plus qu'à isoler Km !
0 = 10.10⁻² × (- Km) + 10.10⁻⁶
- 10.10⁻⁶ = 10.10⁻² × (- Km)
(- 10.10⁻⁶) / 10.10⁻² = - Km
Km = 10.10⁻⁶ / 10.10⁻²
Km = 10⁻⁴
Voilà, j'espère que c'est plus clair pour toi

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
Dr Juiphe aime ce message
 Re: ED 2020-2021
Re: ED 2020-2021
Oui, un grand merci d'avoir pris le temps de tout détailler j'ai bien compris !
Donc à chaque fois que dans un énoncé il n'est pas précisé qu'on est dans le cas d'une cinétique Michaelienne, il faut procéder ainsi avec la fonction affine ?
Donc à chaque fois que dans un énoncé il n'est pas précisé qu'on est dans le cas d'une cinétique Michaelienne, il faut procéder ainsi avec la fonction affine ?

Dr Juiphe- Messages : 210
Date d'inscription : 02/11/2020
Age : 22
Asticoo aime ce message
 Re: ED 2020-2021
Re: ED 2020-2021
Oui, tout à fait !

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
Dr Juiphe aime ce message
 Re: ED 2020-2021
Re: ED 2020-2021
Bonjour,
Je bloque donc sur la derniere étape, comment déterminer le Kmapp de la courbe B?
Merci à vous
Je bloque donc sur la derniere étape, comment déterminer le Kmapp de la courbe B?
Merci à vous
VicVic- Messages : 40
Date d'inscription : 08/10/2020
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !
Le coefficient directeur de la droite est – Km, donc pour déterminer Km on va chercher à calculer le coefficient directeur de cette droite.
Pour ce faire, on utiliser les coordonnées d’un point présent sur le courbe A. Ici, on va prendre un point facile à lire, donc le point d’intersection entre la courbe et l’axe des abscisses, de coordonnées (10.10⁻² ; 0).
Et on utilise ces coordonnées dans l’équation de droite que l’on a trouvées précédemment :
V0 = Vmax – V0/[S] × Km
0 = Vmax – 10.10⁻² × Km
10.10⁻² × Km = Vmax
Km = Vmax / 10.10⁻²
Il nous faut donc également remplacer Vmax. Sachant que Vmax correspond à l’ordonnée à l’origine de notre droite, on n’a qu’à regarder l’ordonnée du point d’intersection entre la courbe et l’axe des ordonnées, ce qui nous donne ici 10.10⁻⁶
D’où
Km = 10.10⁻⁶ / 10.10⁻² = 10⁻⁴
Le Kmapp correspond au Km de la courbe avec inhibiteur, donc on procède exactement de la même façon avec la courbe B. Pour le début, on peut réutiliser les coordonnées du point précédent, puisqu’il est commun aux deux courbes, ce qui donne :
V0 = Vmaxapp – V0/[S] × Kmapp
0 = Vmaxapp – 10.10⁻² × Kmapp
10.10⁻² × Kmapp = Vmaxapp
Kmapp = Vmaxapp / 10.10⁻²
Comme il s’agit d’un inhibiteur incompétitif, la Vmax est également modifiée ! On remplace donc Vmaxapp par la valeur de l’ordonnée à l’origine de la courbe B, qui est 2.10⁻⁶
D’où
Kmapp = 2.10⁻⁶ / 10.10⁻² = 2.10⁻⁴
Est-ce que c'est ok pour toi ?
Le coefficient directeur de la droite est – Km, donc pour déterminer Km on va chercher à calculer le coefficient directeur de cette droite.
Pour ce faire, on utiliser les coordonnées d’un point présent sur le courbe A. Ici, on va prendre un point facile à lire, donc le point d’intersection entre la courbe et l’axe des abscisses, de coordonnées (10.10⁻² ; 0).
Et on utilise ces coordonnées dans l’équation de droite que l’on a trouvées précédemment :
V0 = Vmax – V0/[S] × Km
0 = Vmax – 10.10⁻² × Km
10.10⁻² × Km = Vmax
Km = Vmax / 10.10⁻²
Il nous faut donc également remplacer Vmax. Sachant que Vmax correspond à l’ordonnée à l’origine de notre droite, on n’a qu’à regarder l’ordonnée du point d’intersection entre la courbe et l’axe des ordonnées, ce qui nous donne ici 10.10⁻⁶
D’où
Km = 10.10⁻⁶ / 10.10⁻² = 10⁻⁴
Le Kmapp correspond au Km de la courbe avec inhibiteur, donc on procède exactement de la même façon avec la courbe B. Pour le début, on peut réutiliser les coordonnées du point précédent, puisqu’il est commun aux deux courbes, ce qui donne :
V0 = Vmaxapp – V0/[S] × Kmapp
0 = Vmaxapp – 10.10⁻² × Kmapp
10.10⁻² × Kmapp = Vmaxapp
Kmapp = Vmaxapp / 10.10⁻²
Comme il s’agit d’un inhibiteur incompétitif, la Vmax est également modifiée ! On remplace donc Vmaxapp par la valeur de l’ordonnée à l’origine de la courbe B, qui est 2.10⁻⁶
D’où
Kmapp = 2.10⁻⁶ / 10.10⁻² = 2.10⁻⁴
Est-ce que c'est ok pour toi ?

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
 Re: ED 2020-2021
Re: ED 2020-2021
Bonsoir 
Pour rebondir sur cet exo, quand je fais le calcul du Kmapp = 2*10^-6 / 10*10^-2, je trouve 2*10^-5.
Et ensuite pour calculer le Ki, je trouve un résultat négatif (-1*10^-4).
Je suis parti de la formule du Kmapp = km*(1+I/Ki) et je suis arrivé à Ki = (Km*I)/Kmapp-Km) = (10^-4*8*10^-5) / (2*10^-5 - 10^-4). Est-ce que je me suis trompé ou il y autre méthode ?
Bonne soirée ))
))
Pour rebondir sur cet exo, quand je fais le calcul du Kmapp = 2*10^-6 / 10*10^-2, je trouve 2*10^-5.
Et ensuite pour calculer le Ki, je trouve un résultat négatif (-1*10^-4).
Je suis parti de la formule du Kmapp = km*(1+I/Ki) et je suis arrivé à Ki = (Km*I)/Kmapp-Km) = (10^-4*8*10^-5) / (2*10^-5 - 10^-4). Est-ce que je me suis trompé ou il y autre méthode ?
Bonne soirée
Theomall- Messages : 7
Date d'inscription : 05/12/2020
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !
Pour le calcul du Km il y a effectivement une petite erreur : 2.10⁻⁶ / 10.10⁻² ça fait bien 2.10⁻⁵ ! Mais la méthode est bonne
Ensuite, on a dit plus haut qu'il s'agissait d'un inhibiteur de type incompétitif, donc on a diminution du Km et de la Vmax d'un même facteur !
Donc Kmapp = Km / (1 + [I]/Ki)
Comme on diminue le Km, on divise par ce facteur, on ne multiplie pas ! (contrairement à un inhibiteur compétitif qui augmente le facteur, donc multiplication).
Voilà, j'espère que c'est plus clair pour toi
Pour le calcul du Km il y a effectivement une petite erreur : 2.10⁻⁶ / 10.10⁻² ça fait bien 2.10⁻⁵ ! Mais la méthode est bonne
Ensuite, on a dit plus haut qu'il s'agissait d'un inhibiteur de type incompétitif, donc on a diminution du Km et de la Vmax d'un même facteur !
Donc Kmapp = Km / (1 + [I]/Ki)
Comme on diminue le Km, on divise par ce facteur, on ne multiplie pas ! (contrairement à un inhibiteur compétitif qui augmente le facteur, donc multiplication).
Voilà, j'espère que c'est plus clair pour toi

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
Theomall aime ce message
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !!
Je comprends pas pourquoi on peut pas appliquer directement la formule du Vmaxapp d’une inhibition anti compétitive ?
A savoir : Vmaxapp = Vmax/(1+[I]/ki)
Merci d’avance
Je comprends pas pourquoi on peut pas appliquer directement la formule du Vmaxapp d’une inhibition anti compétitive ?
A savoir : Vmaxapp = Vmax/(1+[I]/ki)
Merci d’avance
Invité- Invité
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !
Oui effectivement, ça marche aussi très bien !!
Oui effectivement, ça marche aussi très bien !!

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
 Re: ED 2020-2021
Re: ED 2020-2021
Eh bien tu ne peux pas passer de :
Vmaxapp / Vmax = 1 / (1 + [I]/Ki) à Vmax / Vmax = 1 + [I]/Ki (lignes 2 et 3)
Si tu inverses d'un côté de l'équation, tu inverses également de l'autre !
Vmaxapp / Vmax = 1 / (1 + [I]/Ki) à Vmax / Vmax = 1 + [I]/Ki (lignes 2 et 3)
Si tu inverses d'un côté de l'équation, tu inverses également de l'autre !

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
 Re: ED 2020-2021
Re: ED 2020-2021
Quelle formule littérale est-ce que tu obtiens à la fin ?
Normalement ton Ki doit être égal à 2.10⁻⁵
Normalement ton Ki doit être égal à 2.10⁻⁵

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
 Question à propos du Km/Ki
Question à propos du Km/Ki
Salut,
Moi aussi je pensais avoir fait une erreur dans mon calcul pour le Ki mais vous avez noté que Km diminuait aussi or c'est un inhibiteur compétitif donc Km augmente et Vmax reste inchangée. Donc Ki=10^-5 mol/L non?
Merci de votre compréhension
Bonne soirée
DELEBRET Lona
Moi aussi je pensais avoir fait une erreur dans mon calcul pour le Ki mais vous avez noté que Km diminuait aussi or c'est un inhibiteur compétitif donc Km augmente et Vmax reste inchangée. Donc Ki=10^-5 mol/L non?
Merci de votre compréhension
Bonne soirée
DELEBRET Lona
lona.delebret- Messages : 50
Date d'inscription : 24/09/2020
 Re: ED 2020-2021
Re: ED 2020-2021
Salut !
inhibiteur compétitif pour l'exo 1, mais inhibiteur incompétitif pour l'exo 4
inhibiteur compétitif pour l'exo 1, mais inhibiteur incompétitif pour l'exo 4

Asticoo- Messages : 589
Date d'inscription : 22/09/2017
lona.delebret aime ce message
 ED 2020-2021
ED 2020-2021
Ah mince, j'avais pas vu, merci!
lona.delebret- Messages : 50
Date d'inscription : 24/09/2020
Asticoo aime ce message
Tutorat Licence Santé Lille Catho :: L1 - Chimie, Chimie Organique, Chimie Structurale, Génétique et Biochimie :: Questions de cours et d'ED :: BIOCHIMIE
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum


