Régression

Bonjour
Serait-il possible de récapituler les étapes qui doivent être effectuées pour calculer une régression s'il vous plait ? Que doit-on calculer en premier ?
Merci d'avance

Il faut en préalable rentrer les données dans ta calculatrice :

Tu vas dans "data" ;
=> dans la colonne 1, tu rentes la variable contrôlé
=> dans la colonne 2, tu rentres la variable aléatoire

Tu fais ensuite "2nd" puis "data"
Tu vas dans "2-Vars-Stats"
=> tu choisis dans la première ligne xdata L1, dans la deuxième ligne ydata L2
=> tu laisses la fréquence sur one

Et tu trouves ainsi le coefficient "r" ; Sx et Sy ; et p0 (a dans la calculatrice)

Tu calcules la variance de la pente de régression via la formule Sp0² = [(Sy²/Sx²) - p0²] / n-2

Tu fais alors un test de student avec la formule t = (p0 - 0) / Sp0 (attention ici c'est l'écart-type de la pente de régression)

Tu compares au t théorique avec l'alpha correspondant et le ddl = n - 2 avec n nombre de paires

Tu interpréteras ainsi par la suite r²

Merci !

Salut !
En faisant un exercice sur la régression, je me suis aperçue que les arrondis pouvait totalement changer des résultats. A combien estimez vous q'iil faut arrondir s'il vous plait ?
De plus dans l'exercice proposé par la banque de QCM, je ne comprends pas pourquoi vous avez arrondi à 3,02 et non 3,03 car au final je trouve t= 42,1 avec le Sx arrondi à 3,02. Et vous avec Sx= 3,02 vous trouvez t=25,5 donc une grosse différence par rapport à mon calcul....



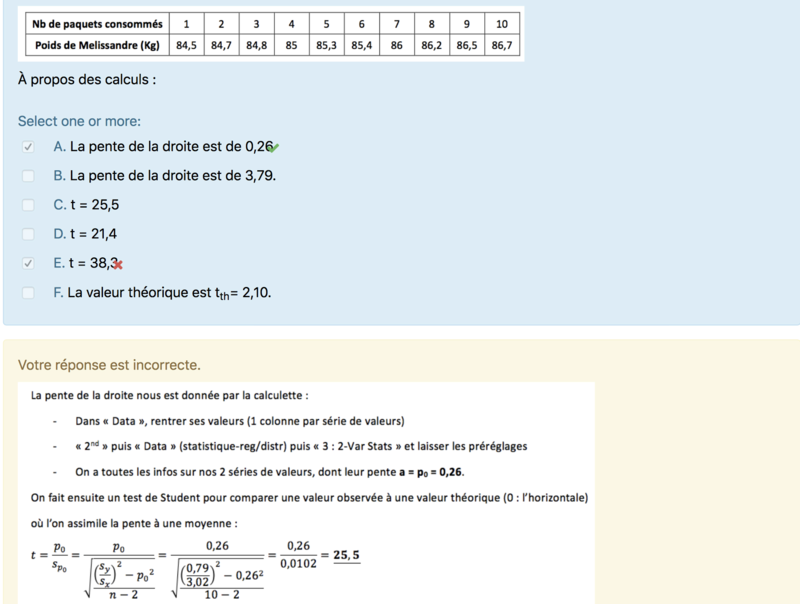
Merci pour votre aide et bonne journée.

ah oui et je ne comprends pas pourquoi cette proposition : "On travaille dans une régression avec X, la variable contrôlée, et Y la variable aléatoire. Si on inverse X et Y, la pente change mais le coefficient de corrélation reste le même." est comptée comme juste car en régression on ne peut pas inverser X et Y normalement ?

Les arrondis c'est toute une histoire dont personne n'a la véritable réponse ! Dans l'idéal il faut toujours être le plus précis possible !

Le Sx arrondi à 3.02 est une troncature je suppose mais effectivement il aurait été plus logique qu'il soit pris à 3.03. Mais pour autant le t est bien de 25,5.

J'aimerais bien voir cette proposition car elle est peu tordue mais pas fausse. en régression X et Y ne sont pas intervertibles mais dans la 2nde partie de la proposition on parle du coeff de corrélation. Or en corrélation si on inverse X et Y la pente change bien (d'où le fait que le graph ne soient pas utilisés) sans changement du coefficient de corrélation.