Concours UE4 2009/2010 - Ex3

Salut !

J'aimerais avoir des précisions pour cet exercice qui m'embrouille un peu.
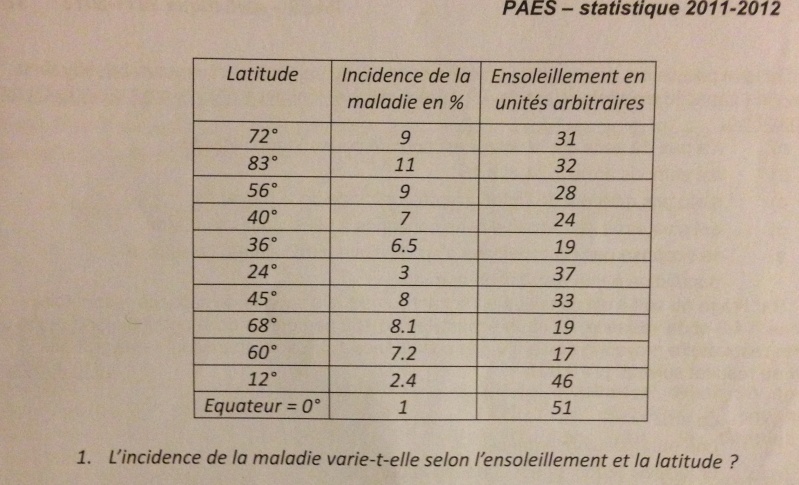
La question semble avoir plusieurs réponses à mon sens, premièrement j'hésite de faire 2 corrélations de Spearman et donc comparer séparément l'incidence-l'ensoleillement et l'incidence-latitude.  Mais j'hésite car pour moi la latitude est une variable contrôlée étant donné qu'on choisit les personnes pas n'importe où. Dans ce cas peut être une régression entre latitude-incidence et corrélation de Spearman entre incidence-ensoleillement  ?

Deuxièmement une comparaison de plusieurs moyennes avec un test non paramétriques (et donc celui de Kruskall Walis) peut aussi répondre à la question ou je me trompe ?

Merci d'avance

Salut Moustik,

J'ai l'impression que ta question ne fait pas masse d'émules, et puisque les jeunes doivent être débordés avec leurs exams, je vais me permettre de te répondre :

Avant de commencer, pour choisir comment répondre à n'importe quelle question statistique, il te faut avoir 2 impératifs statistiques en tête :
Règle d'or n°1 - Il faut s'efforcer de fournir la réponse la plus pertinente à la question, c'est-à-dire la réponse la plus utile au médecin-statisticien qui a construit l'exercice (ou a toi-même plus tard)
Règle d'or n°2 - Il faut s'efforcer de fournir la réponse la plus fiable, c'est à dire associée au risque d'erreur le plus bas possible et donc lié au test le plus puissant réalisable.

La question, qui reste une question classique en santé publique, porte sur la variation d'un paramètre en fonction d'un autre. Si cette variation existe, c'est que les 2 paramètres sont liés. C'est donc une question typique de recherche de lien entre 2 variables.
Les variables sont quantitatives appariées : On est donc dans la catégories des Tests de lien quantitatifs. Ces tests sont souvent mal compris dans le fond alors laisse moi les reprendre rapidement avec toi, pour clarifier les choses :

Sur le versant paramétrique, il existe 2 méthodes : La corrélation de Pearson, et la régression logistique affine avec comparaison des pentes.
Pour appliquer ces tests, il faut que la variabilité de d'un x, ne soit pas affecté par la variabilité de y, ce qui est très difficilement démontrable en réalité.
- La Corrélation de Pearson déduit un coefficient représentant l'étroitesse du lien entre 2 variables x/y.
Ce coefficient est étalonné entre [-1;+1] et l'approche de chacun de ces bornes permet de caractériser la FORCE de ce lien.
- La Régression logistique est une modélisation affine des valeurs (x;y) avec une comparaison de l'écart entre A, la pente de l'équation y=Ax+b et une droite horizontale, signifiant une invariabilité de y quelque soit la valeur de x. Elle permet de déduire une équation affine type y=Ax+B, ce qui permet 2 choses :
- Comparer la pente avec une pente nulle et déceler un lien entre x et y afin d'affirmer l'existence d'un lien.
- Extrapoler une valeur de x en fonction de y, et vice versa, dans l'intervalle d'étude afin d'être PRONOSTIC .
=> Le choix de l'un ou de l'autre doit se faire en fonction de leur UTILITE : Les 2 sont capables d'affirmer un lien mais si vous voulez savoir si le lien est fort, le coefficient de PEARSON est le meilleur paramètre ; Tandis que si vous voulez connaitre une valeur de y pour un x donné dans l'intervalle, l'équation d'une régression affine est la meilleure option.
NB : Ca déduit le pré-admis qu'une régression nécessite une donnée controler, puisqu'il est inutile de déterminer une valeur de y pour une valeur de x, si dans la vraie vie, on est pas capable de manipuler x pour en faire ce qui nous intéresse.

Sur le versant non-paramétrique, il existe la Corrélation de SPEARMAN, qui comme tous les tests non-paramétriques quantitatifs substitue les rangs des données à leurs valeurs numériques afin de gommer les valeurs extrêmes qui impacterait trop une répartition gaussienne (Euh ca je sais pas si c'est clair pour vous...).
Ce test reste une corrélation, avec le même sens que celle de PEARSON, à la différence qu'il s'utilise si les conditions d'applications du coefficient de PEARSON ne sont pas respecté et à votre niveau, ce respect est GRAPHIQUE : Vous devez utiliser ce test que si vous déceler une ABERRATION GRAPHIQUE de la série de variables, à savoir un couple (x;y) complètement en dehors du nuage de point et qui par son existence modifie la courbe de tendance du nuage de point.

Pour en revenir à l'exercice : On cherche un lien entre Incidence et Latitude (1) et Incidence et Ensoleillement (2)

(1) En tant que médecin, ce qui m'intéresserait serait de déterminer un AXE NORD-SUD sur l'incidence de la maladie. La latitude est contrôlable grâce à Airfrance mais je me vois mal demander à mon patient de déménager d'un Tropique à un autre pour diminuer une risque de survenue de sa maladie de 3 %, alors qu'on arrive pas à faire arrêter de boire un cirrhotique... Donc pratiquement, je m'intéresse simplement à "Vivre plus au nord augmente-t-il le nombre de malade ou l'inverse ?", ce qui se traduit par une question d'évaluation de lien avec un intérêt particulier sur la FORCE de ce lien.
Graphiquement, je n'ai pas d'aberrations graphiques sur ces 2 paramètres, je choisis donc d'utiliser pour plus de puissance, le test paramètrique à savoir le coefficient de PEARSON.

(2) Bon la, je n'ai aucune idée de la maladie... Evaluer l'impact de l'ensoleillement sur la dépression ou sur le Cancer épidermoïde de la peau, c'est pas pareil... Après, il me semble plus facile d'inciter un patient à prendre au maximum le soleil ou non que de le faire déménager, donc je serais plus partant pour une REGRESSION.

Pour terminer sur ta dernière question : Un KW ne permet pas seul de déterminer un lien entre plusieurs paramètres, c'est juste un test de comparaison de moyennes. Mais c'est bien que tu vois la stratégie statistique de manière large, continue comme ca : Il existe souvent plus d'une bonne façon de résoudre un problème statistique !

Bon courage pour tes révisions !

Woow je suis impressionné par le fait que t'aies pu prendre le temps de m'expliquer tout ça d'une façon aussi détaillée Franchement bravo et merci !
Du coup tout est clair dans ma tête, enfin je le pense, après réflexion c'est vrai qu'on peut contrôler plutôt l'ensoleillement que la latitude.

T'inquiète pas, avec de bonnes lunettes pour lire ta question, et un bon traitement anti-parkinsonnien pour taper la réponse, je suis capable de tout

Bon courage pour cette dernière ligne droite !

Par contre, je ne comprend pas pourquoi tu utilises de la corrélation de Pearson et non pas une régression ?
Car selon moi, tu ne peux évaluer l'incidence EN FONCTION de la latitude et non pas le contraire. ( La latitude ne varie pas en fonction de l'incidence). Ainsi, la latitude serait le paramètre X contrôlé.

Merci d'avance

Ces deux tests sont bilatéraux : Quand ils déterminent un lien, il ne le réserve pas à une seule façon de l'interpréter.