ED2 2017-2018 Q3

Salut,

Je n'ai pas compris la correction de cet exercice.

On propose un dépistage du cancer colorectal par une analyse de selles (on recherche des traces de sang non visible à l’œil nu dans les selles), on appellera ce test A. 85% des personnes ayant un cancer colorectal ont un test de dépistage positif (= taux de dépistage des malades) et 95% des personnes non malades ont un test négatif.
Si on réalise le test de dépistage A à 1000 personnes atteintes d’un cancer colorectal, quelle est la probabilité d’avoir entre 840 et 870 personnes qui ont un test positif ?
A – 54%
B – 62%
C – 77%
D – 92%
E – autre réponse

J'ai calculé l'écart-type et j'ai trouvé 0,0113. Ensuite j'ai voulu calculer une fluctuation d'échantillonnage mais dans la correction il y a une autre démarche que je n'ai pas comprise.

p(<84%)
e=0.85-0.84 = 0.01 d’où ε = 0.01 / 0.0113 = 0,886 d’où α= 0.38
p(<84%) = 0.38/2 = 0.19

p(>87%)
e=0.87-0.85 = 0.02 d’où ε = 0.02 / 0.0113 = 1.77 d’où α= 0.08
p(>87%) = 0.08/2 = 0.04

p(84%-87%) = 1 – 0.19 – 0.04 = 0.77 = 77%

Pourquoi on calcule p(<84%) et p(>87%) ?

Finalement j'ai compris. J'aimerai juste savoir pourquoi on calcul epsilon ? Ce n'est pas égal à 1,96 ?

Voilà quand même ce que j'avais répondu:

" Salut,

Le mieux dans ce cas là, si tu n'arrive pas à t'y retrouver c'est de faire un schéma :



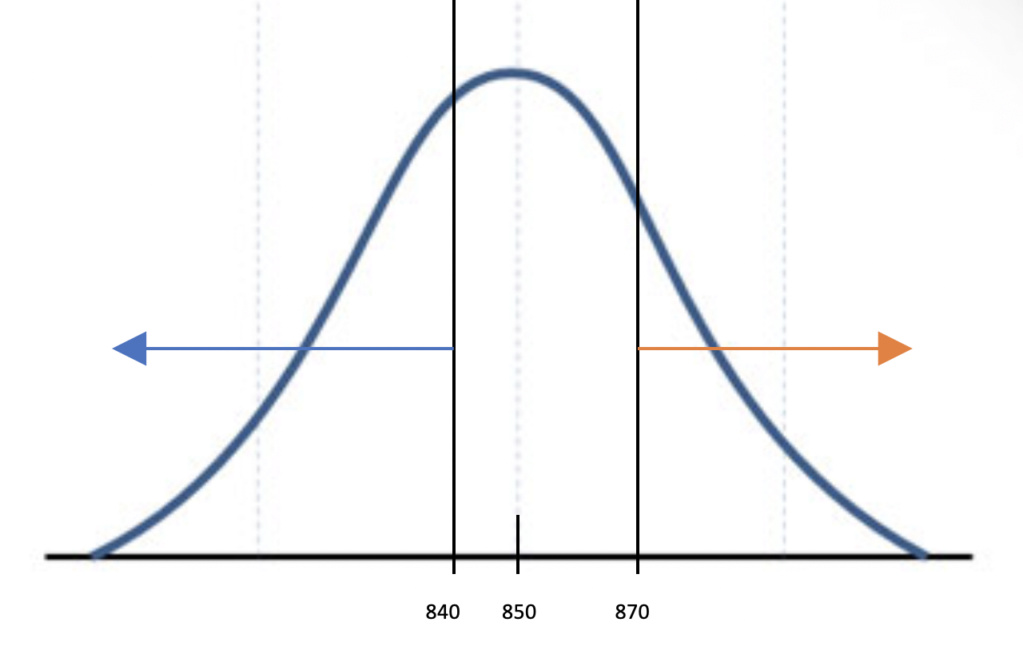
Tu dessines ta courbe de gauss, tu places ta moyenne et tes bornes. Alors comme ton effectif est de 1000, et que tu veux entre 840 et 870, il va donc bien falloir que tu calcules la probabilité d'être à moins de 840 et à plus de 870.

Comme ton effectif est de 1000, 840 personnes parmi 1 000 en pourcentage ça fait bien 84% ((840/1000) x 100 au cas où), et tu vas chercher pour ta borne inférieure la probabilité d'avoir moins de 84% de ton échantillon avec un test +, ce qui est la même chose que la probabilité d'avoir moins de 840 personnes sur 1000 avec un test +.

Même chose pour 870, avec la probabilité d'avoir plus de 87% de ton échantillon avec un test +.

Et après les avoir calculés, tu les soustrais à 1 et tu as la probabilité d'être entre les deux    "

En ce qui concerne ta deuxième question :

Tu cherches une probabilité, tu utilises la formules de l'écart réduit : e = epsilon x s, avec s = racine((pxq)/n)
- e c'est ton écart à la moyenne c'est donc bien  e= 0,85-0,84 pour ta première borne
- s ton écart type avec la formule juste au dessus
- epsilon, ce que tu calcules, est l'indice qui va ensuite te permettre de chercher ta probabilité avec ta table de l'écart réduit (c'est la démarche inverse de celle où tu cherches un epsilon à partir d'un alpha dans ton énoncé)

Ainsi tu trouves ta proba et tu vas pouvoir répondre à la question

Bon courage  

Super je comprends mieux maintenant !
Et pourquoi on a divisé par 2 => p(<84%) = 0.38/2 = 0.19 ?

Ton epsilon va te donner une probabilité en dehors d'un intervalle d'écart e centré sur m, et tu n'as besoin que d'une borne à chaque fois donc tu divises par 2.

OK ! Merci beaucoup