risque alpha et beta

bonjour,
j'ai une question par rapport au tutorat de stats, j'ai noté que le risque alpha et beta n’étaient pas liés par une formule mais qu'il existait
tout de même un lien entre les 2 : Si alpha augmente, Beta diminue.


Si on regarde la formule de l'écart réduit e = epsilon * s et s = rac( p(1-p)/n )
donc epsilon = e / rac(p(1-p)/n)
donc si n augmente, s diminue et epsilon augmente
or dans la table de l’écart réduit, plus epsilon augmente plus alpha diminue
donc si n augmente, alpha diminue

et on sait que Beta diminue quand n augmente.

donc je comprend pas pourquoi on dit que alpha et beta ont une variation qui est opposée

merci d'avance

marco

Avec ca tu comprendras mieux,

Tu vois bien ici que si tu augmente alpha, béta diminuera, et inversement.

(Méa Culpa si je me trompe )

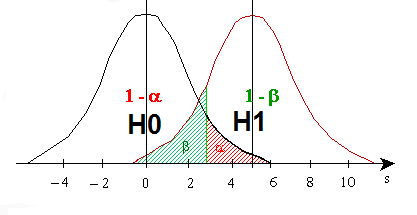
Belle représentation !

Schématiquement :

Si n est constant, alpha est beta varient en sens inverse

Si n augmentent alpha et beta diminuent tous les deux (logique que les risques diminuent lorsque l'on augmente l'échantillon)

Si n diminue alpha et bêta diminuent tous les deux (logique aussi)

Soit tu fais varier le risque soit tu fais varier n mais on ne fait pas varier les deux en même temps.

J'espère que c'est plus clait

[Edit : Jack ayant posté entre deux un parfait résumé, mais j'ai passé du temps à écrire ça alors je le mets quand même

PS : Quand n diminue alpha et bêta augmentent tous deux, erreur d'inattention Jack ]



Bonsoir !

Alpha augmente quand bêta diminue, et inversement, pour N constant.

C'est un fait qui est intéressant quand tu ne cherches pas à rejeter l'hypothèse nulle mais à l'accepter : si je diminue bêta, je diminue le risque de ne pas la rejeter alors qu'il le fallait.

En soi c'est pas essentiel, c'est pas un point important du cours et tous vos exercices sont à alpha = 5%... Mais il arrive qu'on fasse des tests à alpha = 10% dans le but justement de diminuer bêta.

Cela se "voit" bien sur les courbes, merci Lunal



Si tu augmentes N, ton échantillon se rapproche de la population. Ton risque de te tromper est donc moins grand dans un sens comme dans l'autre, comme tu l'as démontré.
Le cas extrême étant un échantillon qui ferait la taille de la population (et donc, qui serait la population entière), tu ne peux pas te tromper dans l'interprétation, ni dans un sens ni dans l'autre...



Tu n'es pas dans le même cas de figure :

Dans le 1er cas, tu as tes données, tu sais ce que tu veux démontrer ou au moins dans quel sens tu veux aller, donc dans quel sens tu ne veux pas te tromper, par exemple :
est-ce que je préfère passer à côté d'un médicament efficace, en étant sûr que ceux que je validerai le sont => Risque alpha diminué
ou est-ce que je ne veux surtout pas passer à côté d'un médicament efficace, quitte à considérer comme efficace des médicaments qui ne le sont pas... => Risque B diminué


Dans le 2nd cas, tu n'as pas encore tes données, et ce que tu veux, c'est trouver un compromis entre ce que va te coûter ton étude statistique (son coût évolue dans le même sens que N, plus tu sondes de gens plus ça te demande de temps et d'argent), et entre la précision de ton résultat (qui évolue aussi dans le même sens que N, ton résultat serait parfait si tu prenais la population entière.
Or le but des statistiques étant de connaître la population à partir d'un échantillon, y'a un moment où il faut trancher entre précision et coût^^.



Voilà

merci beaucoup pour vos explications
j'y vois un peu plus clair maintenant